Tests de significativité : Le test du Chi 2

Il existe plusieurs tests de significativité, les plus usuels sont :
- Les intervalles de confiance
- Le test du Chi 2
- Le test T de student
Le test du Chi 2
Le test du Chi 2 s’applique aux tris croisés, il s’agit de savoir si les différences entre deux sous – échantillons sont significatives. L’interprétation de la valeur du Chi 2 dépend du degré de liberté (noté d.d.l.) qui correspond à :
d.d.l. = (nombre de colonnes – 1) x (nombre de lignes – 1)
Le Chi 2 est la somme des écarts entre les valeurs réelles et les valeurs théoriques du tri croisé. La valeur théorique équivaut à la valeur du sous – échantillon s’il avait répondu de la même manière que l’échantillon global (c’est-à-dire s’il n’y avait pas de différences significatives). Une table de distribution théorique du Chi 2 en fonction du d.d.l. indique le seuil minimum au-dessus duquel les différences sont significatives.
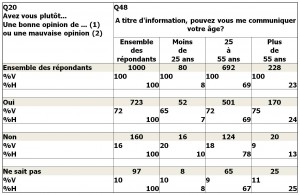
Premier exemple :
valeur du KH12 : 11,8. Degrés de liberté : 4
La valeur théorique est 9,48 pour un d.d.l. de 4 11,8 est supérieur à 9,48. L’âge a donc un effet sur l’opinion.
Les astuces :
Un Chi 2 inférieur au d.d.l. n’est jamais significatif. S’il est supérieur, plus la différence avec le d.d.l. est grande, plus le Chi 2 a de chances d’être significatif.