Tests de significativité : Les intervalles de confiance

Il existe plusieurs tests de significativité, les plus usuels sont :
- Les intervalles de confiance
- Le test du Chi 2
- Le test T de student
Les intervalles de confiance
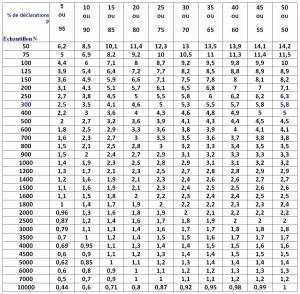
La table de Gauss indique l’intervalle de confiance que l’on peut accorder à un résultat chiffré d’étude en fonction de la taille de l’échantillon, sur base d’échantillons aléatoires.
Le tri plat :
Significativité des Résultats
« La différence est-elle significative ? »
Cette table nous dit que pour un échantillon de 300, les résultats sont fiables à ± 2,5 % pour un résultat net (ex. : 5 % des interviewés ont choisi A) et à ± 5,8 % pour un résultat mitigé (50 % des interviewés ont choisi A).
- ex. : « Quel produit préférez-vous ? »
– A 5 % ± 2,5 %
– B 95 % ± 2,5 % N = 300
B est dans tous les cas meilleur que A.Le problème se pose si l’on a :
– A = 45 % ± 5,8 %
Le score réel de A si l’on avait interrogé l’ensemble de la population aurait pu être compris entre 39,2 % et 50,8 %.- B = 55 % ± 5,8 %
Le score réel de B si l’on avait interrogé l’ensemble de la population aurait pu être compris entre 49,2 % et 60,8 %.Dans les cas extrêmes nous aurions pu avoir
– A = 50,8 %
– B = 49,2 % Ce qui change l’analysePour qu’aucun doute ne soit permis
Il faut que les scores obtenus par l’étude +/- l’intervalle de confiance n’inversent en aucun cas l’ordre initial.